이제부터는 규소 원자 내에 있는 전자들의 특이한 거동을 탐험해 볼까요?

이상한 호텔이 하나 있습니다. 이 호텔은 여러 층으로 되어 있는데, 1층에는 하나의 방이 있고 2층에는 4개의 방이 있으며 3층에는 9개의 방이 있습니다. 각 방은 2명까지만 손님이 투숙할 수 있으며 동성의 손님은 투숙할 수 없습니다. 이상한 점은, 이 호텔에 계단이나 복도나 엘리베이터가 없습니다. 총 14명의 손님이 투숙해 있는데, 1층에 2명, 2층에 8명, 그리고 3층에는 4명이 방을 잡았군요. 손님들은 한 방에 숙박하는 것에 만족하지 않고 수시로 방을 바꿉니다. 1층의 숙박료가 가장 싸고 위층으로 올라갈수록 숙박료가 비싸집니다. 또한, 2층부터는 방이 여러 다른 형태로 되어 있어서 같은 층의 방이라도 숙박료가 달라지기도 합니다. 돈을 더 내면 상위급 방으로 옮길 수 있고, 하위급 방으로 내려가면 돈을 돌려받습니다. 당연히 숙박료는 아무렇게나 책정되어 있지 않고 방마다 일정하게 책정되어 있어서, 방 이동을 할 때는 정확한 액수만큼만 주고받게 됩니다. 이때, 흥미로운 것은 방 이동을 할 때 계단이나 복도나 엘리베이터를 이용하는 것이 아니라, 숙박료 차액을 결제하거나 받은 순간, 손님은 해당 방으로 옮겨져 있습니다. 아무리 짧은 순간이라도 손님이 방과 방 사이에 머물러 있을 수가 없고 항상 방 안에만 있습니다.

이러한 이상한 세상을 양자세상이라고 부릅니다. 이 호텔을 원자라고 생각하면, 각 층은 전자껍질, 손님은 전자, 각 층의 방은 전자궤도, 그리고 숙박료는 전자의 에너지라고 생각하면 됩니다. 각 방의 숙박료는 다른 말로 에너지준위(準位) 또는 에너지레벨이라 불러도 됩니다. 원자 내에 있는 전자는 아무 에너지나 가질 수 없고 띄엄띄엄 한 특정 에너지값만 가질 수 있다는 것을 꼭 기억하세요.

지금까지는 고립된 원자 내에서 전자가 존재할 수 있는 궤도와 해당 궤도의 에너지준위를 설명했습니다. 두 개 이상의 원자가 아주 가깝게 접근을 하는 경우에 전자의 궤도 또는 에너지준위는 어떻게 될까요?

어느 날 우리 태양계와 똑같이 생긴 떠돌이 태양계가 우리 태양계에 아주 가깝게 접근해 오면 어떻게 될까 하는 걱정을 해 본 적이 있을 겁니다. 은하계 간의 충돌은 실제로 일어난다고는 하지만, 우리 평생에는 없을 일이니 너무 걱정하지는 마세요. 그럼, 각각의 태양계 내에 궤도를 돌고 있는 행성 간에 충돌이 없도록 하기 위해서는 어떻게 하면 될까요? 행성들의 궤도가 어떻게 될지 상상해 봅시다. 이때 행성들이 충돌하는 경우는 없다고 가정합니다.

▲ 은하와 은하의 충돌 장면

사진 출처 : 나사

동영상 : 밤하늘 우리 은하와 안드로메다 은하가 충돌하면 이렇게 보인다 (0:18)

영상 출처 : 유튜브 (http://youtu.be/wY65ZrFiR_E)

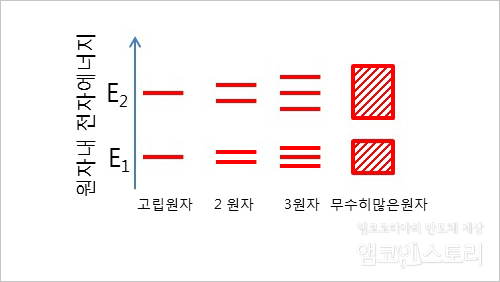
각각의 태양계 내에 있는 행성들의 궤도가 어긋나도록 약간씩 위아래로 변형하면 부딪치는 일은 없겠지요. 마찬가지로, 각 원자 내부의 전자 궤도는 약간씩 위아래로 변형을 일으키게 됩니다. 또 하나의 원자가 접근을 해 오네요. 이 경우에는 전자 궤도가 또 변형하게 됩니다. 셀 수 없이 많은 원자가 접근하게 되면 (실제 우리 주위에서 보는 물질의 경우 셀 수 없이 많은 원자로 이루어져 있지요) 그 수만큼 궤도가 변형을 일으키는데, 일정한 크기의 공간에 수없이 많은 궤도가 중첩되지 않고 들어가게 되면 궤도와 궤도 사이의 간격이 거의 없는 것처럼 보이게 되며, 이것을 연속적인 것으로 간주해서 띠라고 부르게 됩니다. 고립된 원자 내의 전자가 특정 궤도(에너지준위)에 존재하던 것이 고체(수 없이 많은 원자가 아주 가깝게 접근해 있는 상태) 내의 전자는 특정 띠(에너지띠 또는 에너지밴드)에 존재하게 됩니다. 이것이 반도체에서 중요하게 다루고 있는 띠 이론입니다. 사실은 띠 이론을 설명하기 위해서는 고립된 원자 내부의 전자와 고체 내부의 전자가 가지는 에너지를 다뤄야 정확하지만, 독자 여러분의 이해를 돕기 위해서 궤도라는 개념을 가지고 설명하였습니다.

▲ 원자 내 전자에너지 ⓒ백종식

《설국열차》 영화를 보면, 객차마다 다른 계급의 사람들이 승차해 있어서 객차마다 전혀 다른 대우를 받고 있습니다. 뒤쪽 객차에서는 승객들이 앞쪽 객차로 옮겨오기 위해 고군분투하는 모습들이 그려졌지요.

동영상 : 영화 설국열차 뒤쪽 객차의 모습 (0:46)

영상 출처 : 유튜브 (http://youtu.be/IOavCv6OnFU)

우리는 좀 다른 설국열차를 생각해 볼까요?

각각의 객차는 저마다 동력원이 있고 객차와 객차 사이는 연결되어 있지 않고 다만 적당한 사이를 두고 진행하고 있어서 누군가의 도움을 받지 않고는 객차 간 이동이 불가능합니다. 좌석 하나에는 한 사람만 앉을 수 있습니다. 앞쪽 객차는 일등석으로, 좌석과 좌석 사이에 간격이 넓어서 이동에 제약을 받지 않고, 뒤쪽 객차는 삼등석으로 객차 내부가 좌석으로 꽉 차 있어서 빈 좌석이 없으면 이동할 수 없습니다. 출입문은 뒤쪽 객차에만 설치되어 있어서 처음 기차를 탈 때에는 모든 승객이 뒤쪽 객차에 꽉 차게 되며 빈 좌석이 없어서 승객들이 화장실도 갈 수 없습니다. 일등석이 있는 객차로 옮겨가기 위해서는 돈을 지급해야 하고, 일등석에서 삼등석으로 이동하면 반대로 돈을 돌려받는다고 가정하지요. 객차 간 요금의 차이는 객차가 떨어져 있는 사이가 넓을수록 큽니다. 어떤 경우에는 객차 간 간격이 없을 수가 있는데, 이럴 때에는 아주 적은 돈을 지불하고도 앞쪽 객차로 옮겨갈 수 있겠지요. 어떤 경우에는 객차 간 간격이 너무 멀어서 앞쪽 객차로 옮겨가는 것이 거의 불가능할 수도 있겠습니다.

앞뒤 객차 모두 좌석이 있어 승객이 앉을 수 있으니 이를 허용대(許容帶)라고 부르지요. 객차와 객차 사이에는 사람들이 탈 수 있는 좌석이 없어서 금지대라고 부르기로 합니다. 처음에 승객이 탑승했을 때 앞쪽 객차에는 승객이 아무도 없었으므로 공핍대라고 부르고, 뒤쪽 객차에는 좌석 수만큼 승객을 가득 채워서 태웠으므로 충만대라고 부르기로 합니다. 객차와 객차 사이의 거리를 밴드갭이라고 부르며, 이 크기에 따라 객차 간 이동 시 지급하거나 돌려받아야 하는 돈의 양이 정해집니다.

뒤쪽 객차에서 앞쪽 객차로 승객이 이동할 때에는, 가장 앞쪽 좌석의 승객에게 우선권이 있습니다. 왜냐하면, 모든 좌석이 꽉 차 있는 상태에서 뒤쪽 좌석의 승객은 앞쪽으로 올 수가 없겠지요. 일단, 앞쪽 좌석의 승객이 앞쪽 객차로 돈을 지급하고 이동하게 되면 그 좌석은 비게 됩니다. 좌석이 비었다는 것은 이제부터 뒤쪽 객차에서도 승객들이 이동할 수 있다는 뜻입니다. 하지만 좀 복잡하겠군요. 한 사람씩 빈자리를 채우는 방법으로 이동해야 하니 시간이 좀 걸리겠습니다. 하지만 빈자리가 늘어날수록 승객들이 이동하기는 더 수월해질 것입니다. 이것을 반도체의 띠 이론에서 그림으로 나타낸 것이 아래에 있습니다.

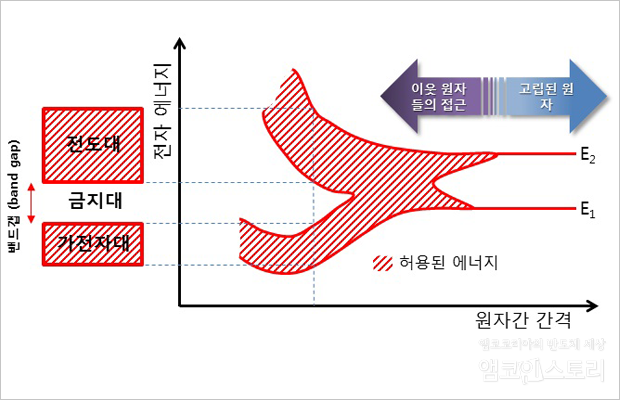
그림에서 보는 대로, 빗금 친 영역 내부를 전자가 존재할 수 있는 띠라고 해서 허용대(‘띠’를 한자어로 하면 ‘대’가 됩니다)라고 부르고, 허용대 사이에 전자가 존재할 수 없는 영역을 금지대라고 부르며, 이 금지대의 간격을 밴드갭(band gap)이라고 부릅니다. 허용대는 전자가 가득 차 있는 충만대(充滿帶)와 전자가 없는 공핍대(空乏帶)로 나뉩니다.

전자가 밴드갭 이상의 에너지를 얻으면 충만대에서 공핍대로 이동하게 됩니다. 이 공핍대에서는 전자가 자유로이 이동할 수 있어서 전류를 흐르게 하므로 전도대라고 부릅니다. 충만대에서 공핍대로 전자가 에너지를 얻어서 이동하게 되면 충만대에 빈자리가 생기고 이 빈자리를 정공이라고 부릅니다. 이 빈자리에는 이웃 전자가 이동해 올 수 있고, 그로 인해 새롭게 생긴 빈자리는 또 다른 전자가 이동해 올 수 있습니다. 이런 방법으로 빈자리는 움직일 수 있게 되며, 이 빈자리는 전자가 움직이는 것의 반대로 움직이게 됩니다. 여러분은 이제 반도체의 특성을 설명하는 띠 이론(밴드이론)을 이해하게 되었습니다.

▲ 전자에너지와 원자 간 간격을 나타낸 표 ⓒ백종식

지난 호에 도체, 반도체, 부도체의 구분을 전기적 특성을 가지고 설명을 해보았습니다. 이제 띠 이론을 가지고 다시 한 번 도체, 반도체, 부도체의 전기적인 특성을 설명해 볼까요?

금속의 경우에는 금지대가 존재하지 않아 두 개의 허용대가 겹쳐져 있습니다. 즉, 언제나 전류를 흐르게 할 수 있습니다. 부도체의 경우에는 금지대의 밴드갭이 매우 커서 보통 전자가 공핍대에 올라갈 수가 없어 모든 전자가 충만대에 존재하고 어떤 전자도 움직일 공간이 없으니 전류를 흐르게 하지 않습니다. 반도체는 금지대가 존재하지만 밴드갭이 크지 않아 적당한 에너지를 공급해주면 충만대의 전자가 공핍대로 올라가 자유롭게 이동할 수 있게 되며, 또한 충만대에 빈자리(정공)를 만들어 정공도 이동(사실은 정공이 이동하는 것이 아니고 이웃 전자들이 정공을 채워나가는 것)을 할 수 있게 되어 전류를 흐르게 합니다. 하지만 반도체의 경우에는 금속과 달리 공핍대에 올라가는 전자의 수가 제한적으로만 있어서 금속만큼 전류를 잘 흐르게 하지는 못합니다.